How to Play
Before I introduce the problem, I pass out some Post-its. One pad of Post-its is enough for a group of students to try the problem several times.
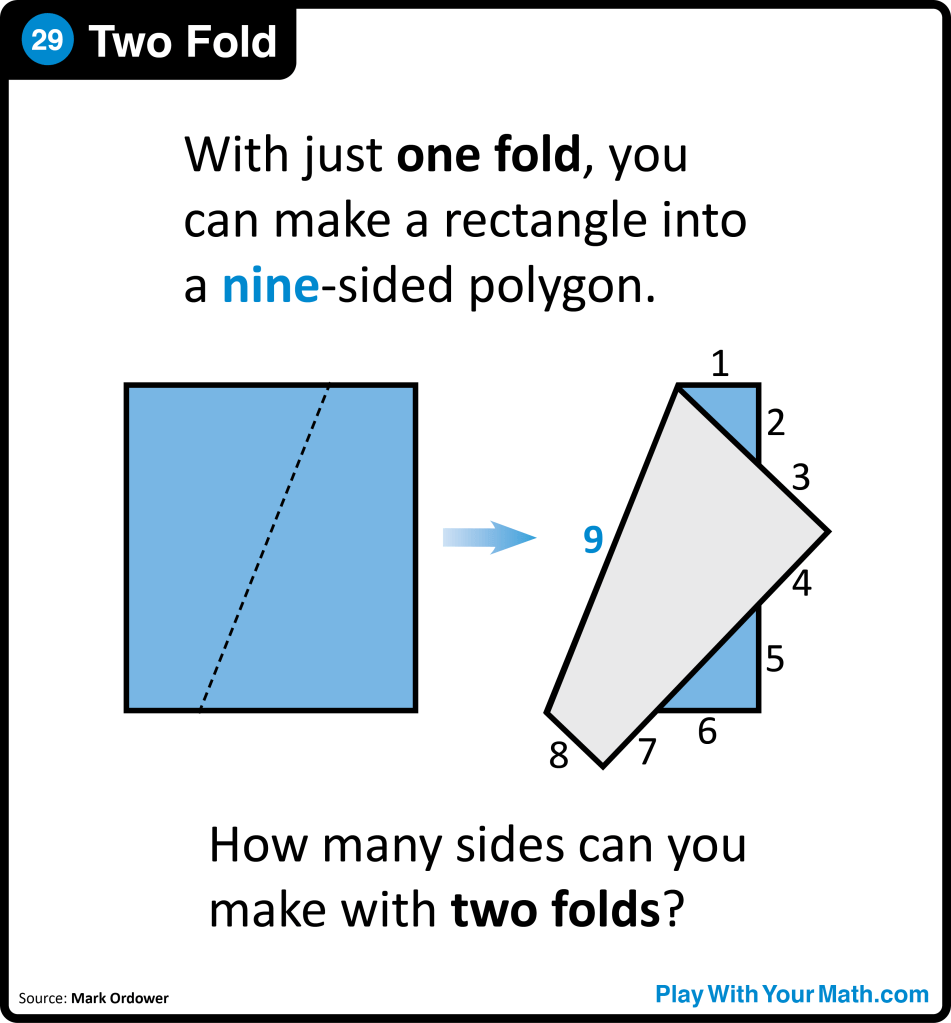
Attempt 1: I first ask students to fold the Post-it once in any way they want. Then, I ask them to count how many sides this new polygon has. I might model with a full-sized piece of paper. I’d take a moment to poll the crowd, and I usually get answers ranging from 3-9.
Attempt 2: I ask them to grab a new Post-it and try again, this time trying to make the most sides possible. After a moment, I ask them to share out again and acknowledge that the most is 9 sides, projecting the image from the poster.
Attempts 3+: I ask them to grab a new Post-it, fold it twice, and count the sides. At this point, I revealing the core question: what is the maximum number of sides you can get with two folds?
Tasting Notes
Start small: Instead of looking for the most sides, look for any possible number of sides. Can you make a 7 sided polygon? An 11 sided polygon? Fill in the gaps.
Be exhaustive: Look at the once-folded polygon and draw lines to show the different ways to fold it. How many different ways to fold it are there? If the first fold was different, would those options be different?
What is a fold? When I was exploring this problem myself, I tried to use paper and pencil to make sense of folding paper. I wondered if a fold is like a cut and explored what happens when a polygon is cut with a straight line. I wondered if a fold is like overlapping polygons, and how many sides result if two polygons overlap in different ways. I haven’t asked students to explore these questions (yet) but I had fun with them.
Still searching: When I share this problem with people/students, their initial engagement is often short lived. I’m still playing with how I can support and encourage sustained play, and I hope to update this when I find something satisfying. If you have ideas, please share!
Where It Comes From
I saw this TikTok from Marc Odower, in January and saved it until I had time to play, which ended up being during our state tests. I was immediately hooked, drafted a poster, and sent it to CiCi. It was the least terrible test proctoring experience I’ve had.
After we had thoroughly played with the problem, I went back to the TikTok and checked the comments to see if there were solutions. I was delighted to see that not only were the answers all over the place, but even Marc had commented with uncertainty.

Why it matters
Try again and again: Like Pentagram, this is a quick problem that you can try many many times. And in both problems, I ended up trying the same thing several times. It creates a need for being systematic without an obvious way to try every possibility.
Folding is physical: Like Eightfold, this problem is tactile and requires dexterity, which is a nice change of pace from the normal modes of doing math.
Prove it: Part of the play is trying to convince yourself or others that you’ve found the most sides. I’m still not convinced I have the solution. I have conjectures, but I’m not 100% sure. And I love/hate that.
Variations
Change the shape: I wonder if a triangle would be interesting?
Keep folding: I wonder how many sides you can make with 3 folds?
